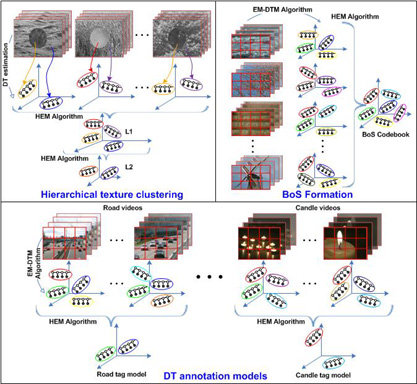
In this project, we address the problem of clustering dynamic texture (DT) models, i.e., clustering linear dynamical systems (LDS). Given a set of DTs (e.g., each learned from a small video cube extracted from a large set of videos), the goal is to group similar DTs into several clusters, while also learning a representative DT “center” that can sufficiently summarize each group. This is analogous to standard K-means clustering, except that the datapoints are dynamic textures, instead of real vectors.
The parameters of the LDS lie on a non-Euclidean space (non-linear manifold), and hence cannot be clustered directly with the K-means algorithm, which operates on real vectors in Euclidean space. An alternative to clustering with respect to the manifold structure is to directly cluster the probability distributions of the DTs. One method for clustering probability distributions, in particular, Gaussians, is the hierarchical expectation-maximization (HEM) algorithm, proposed in [Vasconcelos & Lippman, NIPS’98]. The original HEM algorithm takes a Gaussian mixture model (GMM) and reduces it to another GMM with fewer components, where each of the new Gaussian components represents a group of the original Gaussians (i.e., forming a cluster of Gaussians).
In this project, we derive an HEM algorithm for clustering dynamic textures through their probability distributions. The resulting algorithm is capable of both clustering DTs and learning novel DT cluster centers that are representative of the cluster members, in a manner that is consistent with the underlying generative probabilistic model of the DT. A robust DT clustering algorithm has several applications in video and motion analysis, including: 1) hierarchical clustering of motion; 2) video indexing for fast video retrieval; 3) DT codebook generation for the bag-of-systems motion representation; 4) semantic video annotation via weakly-supervised learning. DT clustering can also serve as an effective method for learning DTs from a large dataset of video via hierarchical modeling. Finally, DT clustering can also be applied to semantic music annotation, where each concept is modeled by a mixture of DTs.
Selected Publications
- Clustering Dynamic Textures with the Hierarchical EM Algorithm for Modeling Video.
,
IEEE Trans. on Pattern Analysis and Machine Intelligence (TPAMI), 35(7):1606-1621, Jul 2013. [appendix] - Clustering Dynamic Textures with the Hierarchical EM Algorithm.
,
In: IEEE Conf. Computer Vision and Pattern Recognition (CVPR), San Francisco, Jun 2010. [supplemental]
Music Applications
- A Bag of Systems Representation for Music Auto-tagging.
,
IEEE Trans. on Audio, Speech and Language Processing (TASLP), 21(12):2554-2569, Dec 2013. - Time Series Models for Semantic Music Annotation.
,
IEEE Trans. on Audio, Speech and Language Processing (TASLP), 19(5):1343-1359, Jul 2011. - Automatic music tagging with time series models.
,
In: International Society for Music Information Retrieval Conference (ISMIR), Utrecht, Aug 2010.
