Gaussian Mixture Models (GMMs) are considered to be an universal approximator for any continuous probabilistic distribution. Normally, mixture models with a large number of components more accurately characterize irregular and multimodal distributed data. Hence, a GMM with enough number of components could be a generic approximate distribution in probabilistic modelling and inference.
However, it’s inefficient to model with GMM having large number of components in practice. Furthermore, intractability probably would happen during inference. For example, a weighted kernel density estimation (KDE) can be considered as a mixture model with the number of components equal to the number of data points N. The likelihood computation of a new test data will be time consuming when N is extremely large, which is common with the advent of social networks and cloud computing. On the other hand, when the Product Rule is used in probabilistic inference, the number of mixture components will increase exponentially .
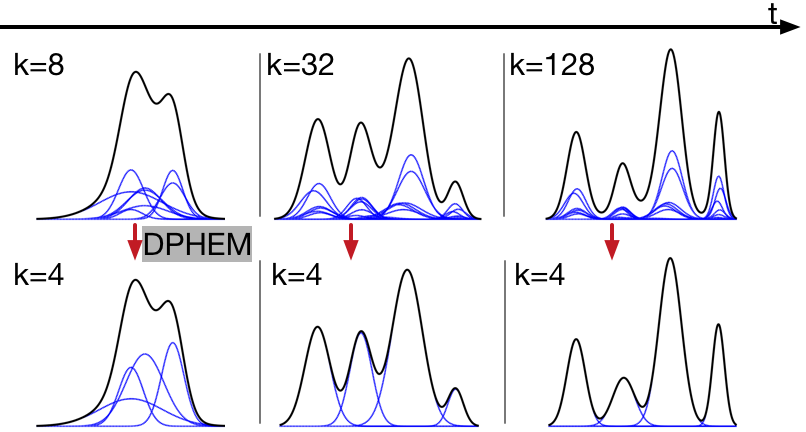
In this project, we propose an algorithm for simplifying the GMM into a reduced mixture model with fewer mixture components. The reduced model is obtained by maximizing a variational lower bound of the expected log-likelihood of a set of virtual samples. We develop three applications for our mixture simplification algorithm: recursive Bayesian filtering using Gaussian mixture model posteriors, KDE mixture reduction, and belief propagation without sampling. For recursive Bayesian filtering, we propose an efficient algorithm for approximating an arbitrary likelihood function as a sum of scaled Gaussian. Experiments on synthetic data, human location modeling, visual tracking, and vehicle self-localization show that our algorithm can be widely used for probabilistic data analysis, and is more accurate than other mixture simplification methods.
Selected Publications
- Approximate Inference for Generic Likelihoods via Density-Preserving GMM Simplification.
,
In: NIPS 2016 Workshop on Advances in Approximate Bayesian Inference, Barcelona, Dec 2016. - Density-Preserving Hierarchical EM Algorithm: Simplifying Gaussian Mixture Models for Approximate Inference.
,
IEEE Trans. on Pattern Analysis and Machine Intelligence (TPAMI), 41(6):1323-1337, June 2019.
