Clustering hidden Markov Models (HMMs)

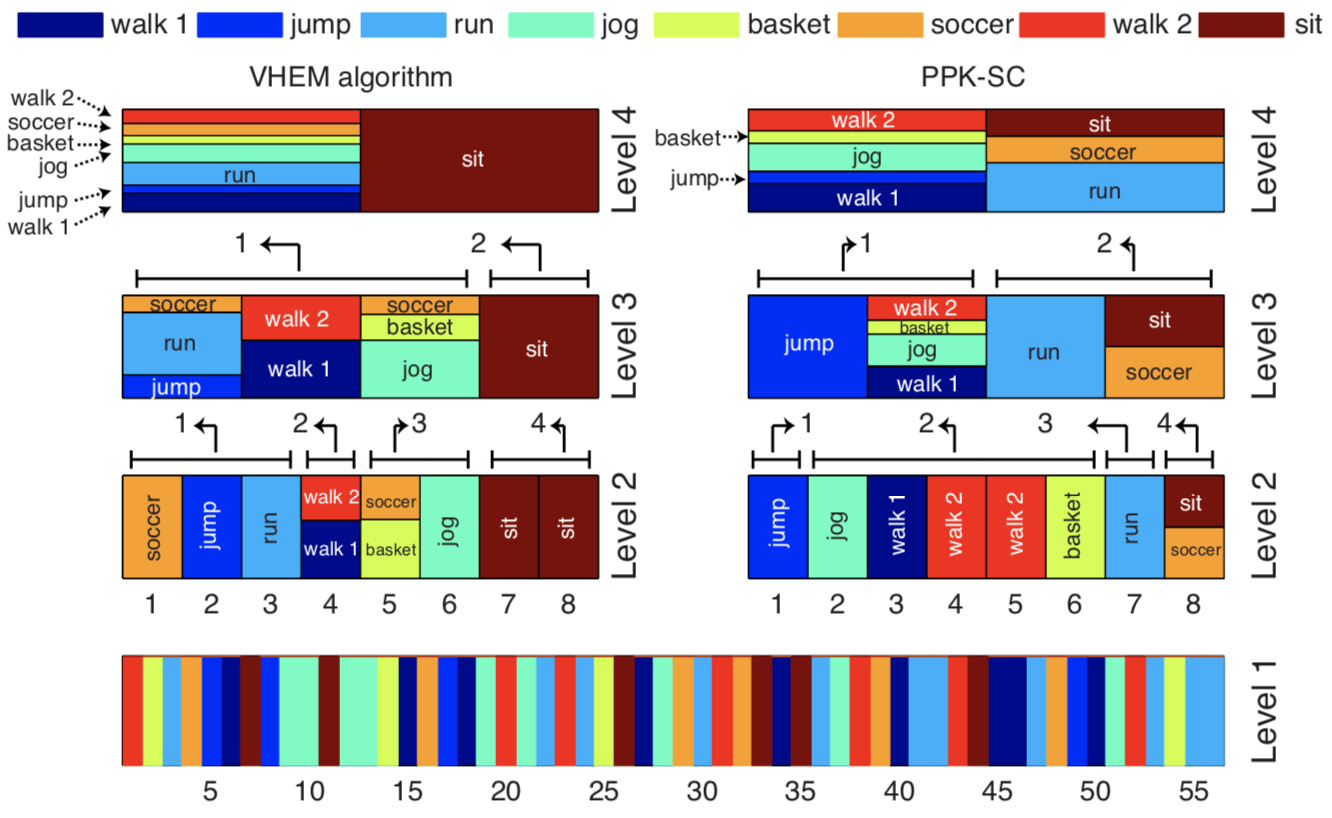
The hidden Markov model (HMM) is a widely-used generative model that copes with sequential data, assuming that each observation is conditioned on the state of a hidden Markov chain. In this project, we derive a novel algorithm to cluster HMMs based on the hierarchical EM (HEM) algorithm. The proposed algorithm i) clusters a given collection of HMMs into groups of HMMs that are similar, in terms of the distributions they represent, and ii) characterizes each group by a “cluster center”, that is, a novel HMM that is representative for the group, in a manner that is consistent with the underlying generative model of the HMM. To cope with intractable inference in the E-step, the HEM algorithm is formulated as a variational optimization problem, and efficiently solved for the HMM case by leveraging an appropriate variational approximation. The benefits of the proposed algorithm, which we call variational HEM (VHEM), are demonstrated on several tasks involving time-series data, such as hierarchical clustering of motion capture sequences, and automatic annotation and retrieval of music and of online handwriting data, showing improvements over current methods. In particular, our variational HEM algorithm effectively leverages large amounts of data when learning annotation models by using an efficient hierarchical estimation procedure, which reduces learning times and memory requirements, while improving model robustness through better regularization.

In follow-up work, we also propose a novel HMM-based clustering algorithm, the variational Bayesian hierarchical EM algorithm, which clusters HMMs through their densities and priors, and simultaneously learns posteriors for the novel HMM cluster centers that compactly represent the structure of each cluster. The numbers of clusters and states, K and S, are automatically determined in two ways. First, we place a prior on the pair (K; S) and approximate their posterior probabilities, from which the values with the maximum posterior are selected. Second, some clusters and states are pruned out implicitly when no data samples are assigned to them, thereby leading to automatic selection of the model complexity. Experiments on synthetic and real data demonstrate that our algorithm performs better than using model selection techniques with maximum likelihood estimation.