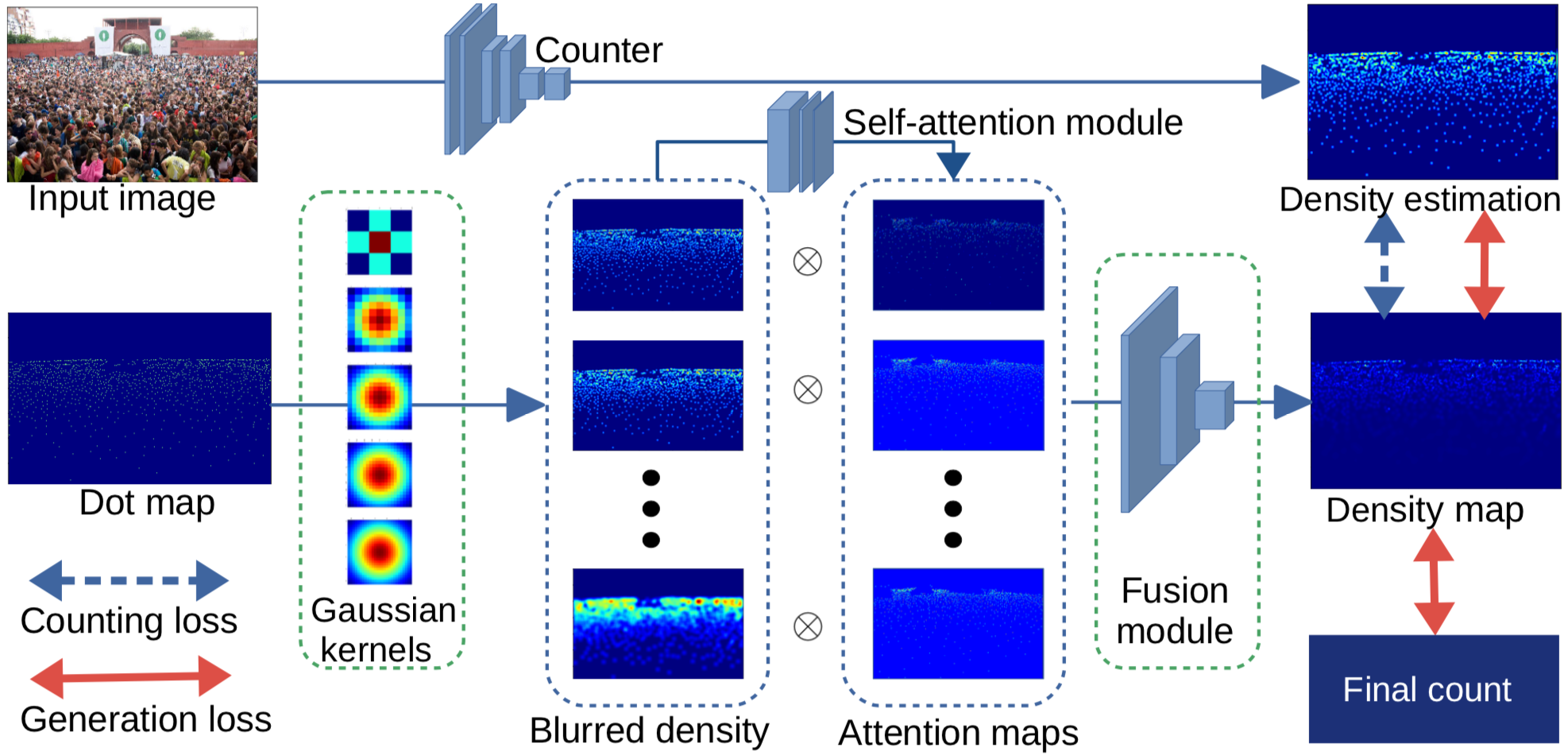
Adaptive Density Map Generation for Crowd Counting

Crowd counting is an important topic in computer vision due to its practical usage in surveillance systems. The typical design of crowd counting algorithms is divided into two steps. First, the ground-truth density maps of crowd images are generated from the ground-truth dot maps (density map generation), e.g., by convolving with a Gaussian kernel. Second, deep learning models are designed to predict a density map from an input image (density map estimation). Most research efforts have concentrated on the density map estimation problem, while the problem of density map generation has not been adequately explored. In particular, the density map could be considered as an intermediate representation used to train a crowd counting network. In the sense of end-to-end training, the hand-crafted methods used for generating the density maps may not be optimal for the particular network or dataset used. To address this issue, we first show the impact of different density maps and that better ground-truth density maps can be obtained by refining the existing ones using a learned refinement network, which is jointly trained with the counter. Then, we propose an adaptive density map generator, which takes the annotation dot map as input, and learns a density map representation for a counter.  The counter and generator are trained jointly within an end-to-end framework.

The adaptive generation method presented above has three disadvantages:

  1. The summation of the generated density map is not always equal to the people count since the fusion network may cause the sum to deviate.
  2. Gaussian kernels are not suitable for density map generation, especially for objects like vehicles since the shape of vehicles is not match with Gaussian kernels.
  3. It is difficult to analyze the kernel shape of individuals since the density map is generated directly.

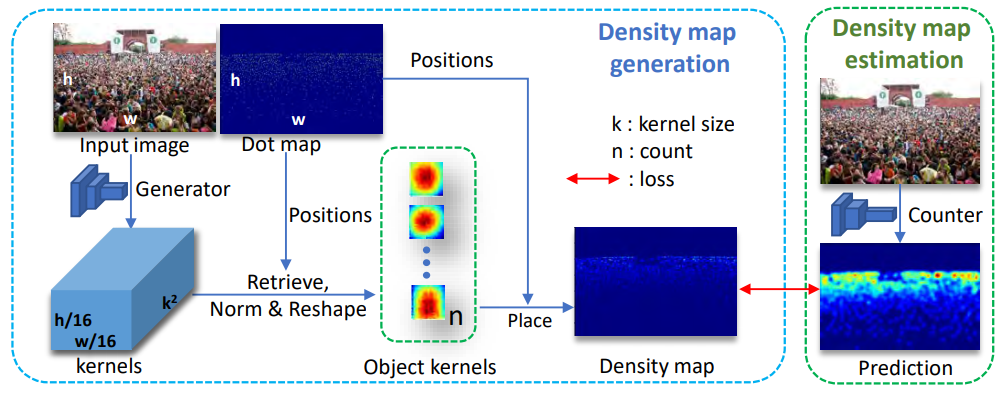
We propose a novel generation framework to overcome these problems. In particular, we generate density kernels for each object and form the density map based on the positions of these objects. The kernels are always normalized (sum to 1) so that the summation of the learned density map is always equal to the number of objects. Furthermore, the kernel shapes are easy to analyze since they are generated explicitly for each object. Finally, the shape of kernels can adapt to different objects so the proposed framework can naturally apply to general object counting tasks.

The experiment results on popular counting datasets confirm the effectiveness of the proposed learnable density map representations.

Selected Publications

Results/Code