Most crowd counting algorithms utilize a deep network to predict density maps from crowd images, where the sum over a region in the density map is the prediction of the count in that region. Most methods treat this problem as a standard regression task, using the standard L2 norm between the ground-truth and predicted density maps as the loss function. Besides L2-norm, Bayesian loss (BL) consider an annotation-wise loss function, based on point supervision.
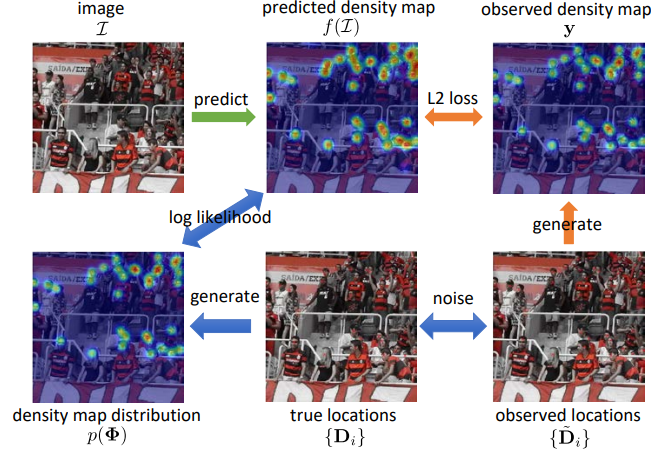
However, both L2 and BL have two deficiencies. First, the noise in the annotation process is not considered in a principled way. L2 and BL make an assumption about per-pixel i.i.d. Gaussian additive noise on the observed density value. However, the noise in the density map arises from the noise in the human annotations (i.e., the displacement of the annotated locations), which in general should not lead to i.i.d Gaussian noise observation noise. Second, the correlation between pixels is ignored. L2 and BL assume independence between pixels in the density map. However, if an annotation moves, the changes in the density map in nearby pixels are correlated.
To address these issues, we proposed a novel loss function that explicitly models annotation noise as random variables. Instead of considering the human annotations as the “ground-truth” locations, we consider the annotations as noisy observations of the true person locations. The annotation noise around the true locations induces a joint probability distribution over density maps. First, we derive the form of the marginal probability distribution of the crowd density value at a spatial location in the density map. However, due to its intractability, we propose to approximate this marginal distribution using a Gaussian distribution, leading to an approximation to the joint probability density based on products of marginals. In order to model correlations between pixels, we then derive an approximation to the joint probability distribution using a multivariate Gaussian distribution with full covariance matrix. As the multivariate Gaussian has dimension equal to the size of the image, we then propose a low-rank method to approximate the covariance matrix, which reduces computational complexity. Finally, the negative log-likelihood of the m.v. Gaussian is used as the loss function for training the density map estimator.
The proposed loss function decomposes into a per-pixel weighted L2-norm term and a correlation term. In the per-pixel weighted term, the loss will reduce the weight for uncertain regions, as compared to the L2 loss (which uses equal weights). Therefore, the proposed loss function is robust to annotation noise and the predicted high-density regions are allowed to move around to find a consistent location. The second term models the correlations between pixels in high-density regions, which can improve training of the density map estimator.
We use our loss function to train a crowd density map estimator and achieve state-of-the-art performance on three large-scale crowd counting datasets, which confirms its effectiveness. Examination of the predictions of the trained model shows that it can correctly predict the locations of people in spite of the noisy training data, which demonstrates the robustness of our loss function to annotation noise.
Selected Publications
,
In: Neural Information Processing Systems (NeurIPS), Dec 2020. [supplemental]
,
IEEE Trans. Pattern Analysis and Machine Intelligence (TPAMI), 45(12):15065-15080, Dec 2023 (online Jul 2023).
Results/Code
- Result for noisy crowd counting.
- Code is available here.