Bayesian inference is a principled method to estimate the uncertainty of probabilistic models. In most applications, especially in deep learning, the likelihood model and model prior are not conjugate hence marginalizing over model prior or posterior cannot be performed analytically, which hinders the practical applicability. Approximate inference methods, such as Markov chain Monte Carlo and variational inference, will approximate the posterior while keeping inference tractability. However, even though a decent approximation of posterior can be obtained, the computation of predictive distribution is usually intractable due to loss of conjugacy, and is of high cost if tractable.
The predictive distribution (a categorical distribution for classification) is typically approximated using Monte Carlo integration using samples from the posterior. However, to perform the computation, we need to maintain a large number of samples, repeatedly evaluate the model and finally average the model outputs. This problem is impractical in many real-world cases.
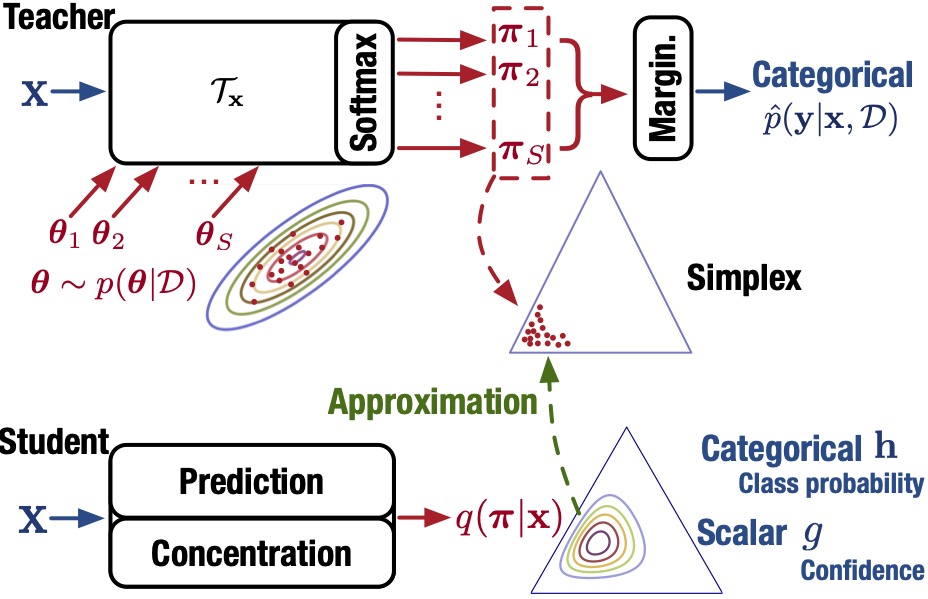
In this work, aiming at boosting the prediction speed while maintaining a rich characterization of the prediction, we propose to approximate the distribution of class probabilities over the simplex induced by the model posterior in an amortized fashion. This naturally diverts the heavy-load MC integration process from testing period to approximation period. Different from the previous work in Bayesian knowledge distillation, which only focuses on the output categorical distribution (a point on simplex), the induced distribution over the simplex provides: 1) rich knowledge including prediction confidence for identifying out-of-domain (OOD) data; 2) the possibility to use more expressive distributions as the approximate model.
We term the Bayes classifier as “Bayes teacher” and the approximate distribution as “student”, due to the analogy with teacher-student learning. A Dirichlet distribution is used as the student due to its expressiveness, conjugacy to categorical distribution and its efficient reparameterization for training. We propose to explicitly disentangle the parameters of the student into a prediction model (PM) and concentration model (CM), which capture class probability and sharpness of Dirichlet respectively. The CM output can directly be used as a measure for detecting OOD data. We term our method as One-Pass Uncertainty (OPU) as it simplifies real-world evaluation of Bayesian models by computing the predictive distribution with only one model evaluation.
Empirical evaluations show a significant speedup (500 x) of Bayes models. The results on Bayes NN show that OPU performs better in misclassification detection and OOD detection than state-of-the-art works in Bayesian knowledge distillation. It can also be observed that explicit disentangling of mean and concentration helps improve the performance. The comparisons of different probability measures validate the theoretical analysis. We also conduct empirical evaluations and comparisons on Bayes logistic regression and Gaussian process, to show OPU is universally applicable to all Bayesian classification models.
Selected Publications
,
IEEE Transactions on Neural Networks and Learning Systems (TNNLS), 33(4):1492-1506, Apr 2022 (online 2020).
