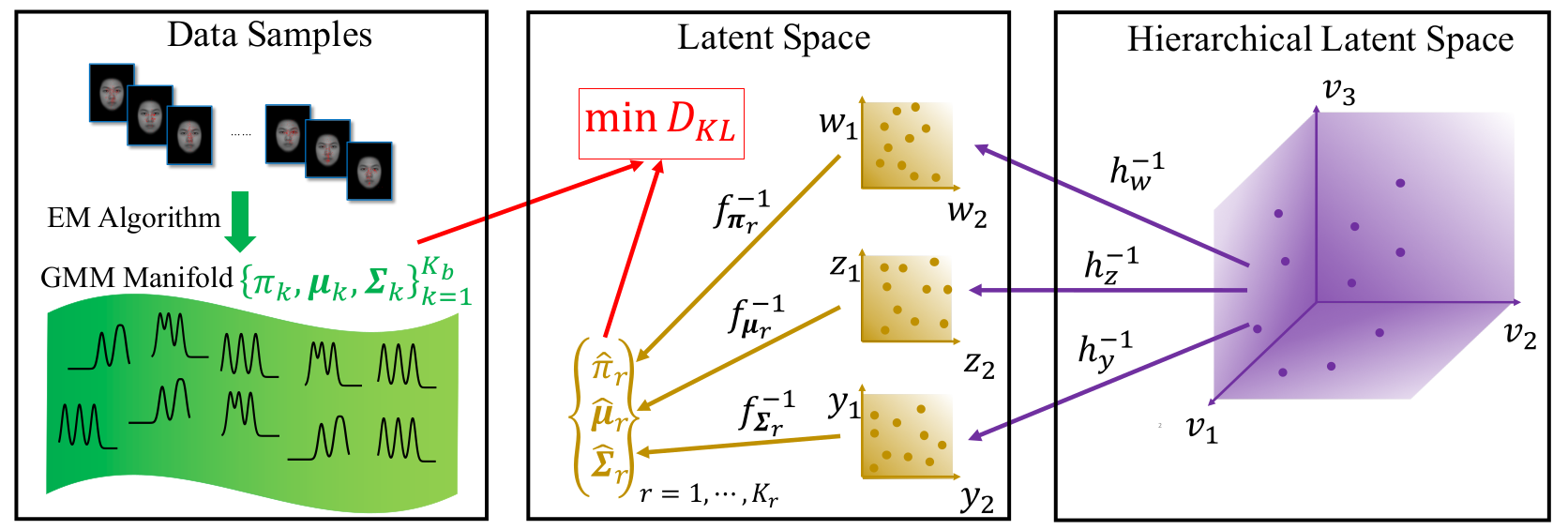
 The Gaussian Mixture Model (GMM) is among the most widely used parametric probability distributions for representing data. However, it is complicated to analyze the relationship among GMMs since they lie on a high-dimensional manifold. Previous works either perform clustering of GMMs, which learns a limited discrete latent representation, or kernel-based embedding of GMMs, which is not interpretable due to difficulty in computing the inverse mapping. In this paper, we propose Parametric Manifold Learning of GMMs (PML-GMM), which learns a parametric mapping from a low-dimensional latent space to a high-dimensional GMM manifold. Similar to PCA, the proposed mapping is parameterized by the principal axes for the component weights, means, and covariances, which are optimized to minimize the reconstruction loss measured using Kullback-Leibler divergence (KLD). As the KLD between two GMMs is intractable, we approximate the objective function by a variational upper bound, which is optimized by an EM-style algorithm. Moreover, We derive an efficient solver by alternating optimization of subproblems and exploit Monte Carlo sampling to escape from local minima. We demonstrate the effectiveness of PML-GMM through experiments on synthetic, eye-fixation, flow cytometry, and social check-in data.
The Gaussian Mixture Model (GMM) is among the most widely used parametric probability distributions for representing data. However, it is complicated to analyze the relationship among GMMs since they lie on a high-dimensional manifold. Previous works either perform clustering of GMMs, which learns a limited discrete latent representation, or kernel-based embedding of GMMs, which is not interpretable due to difficulty in computing the inverse mapping. In this paper, we propose Parametric Manifold Learning of GMMs (PML-GMM), which learns a parametric mapping from a low-dimensional latent space to a high-dimensional GMM manifold. Similar to PCA, the proposed mapping is parameterized by the principal axes for the component weights, means, and covariances, which are optimized to minimize the reconstruction loss measured using Kullback-Leibler divergence (KLD). As the KLD between two GMMs is intractable, we approximate the objective function by a variational upper bound, which is optimized by an EM-style algorithm. Moreover, We derive an efficient solver by alternating optimization of subproblems and exploit Monte Carlo sampling to escape from local minima. We demonstrate the effectiveness of PML-GMM through experiments on synthetic, eye-fixation, flow cytometry, and social check-in data.
Publications
- PRIMAL-GMM: PaRametrIc MAnifold Learning of Gaussian Mixture Models.
,
IEEE Trans. on Pattern Analysis and Machine Intelligence (TPAMI), 44(6):3197-3211, June 2022 (online 2021). [code] - Parametric Manifold Learning of Gaussian Mixture Models.
,
In: International Joint Conference on Artificial Intelligence (IJCAI), Macau, Aug 2019.
Result
