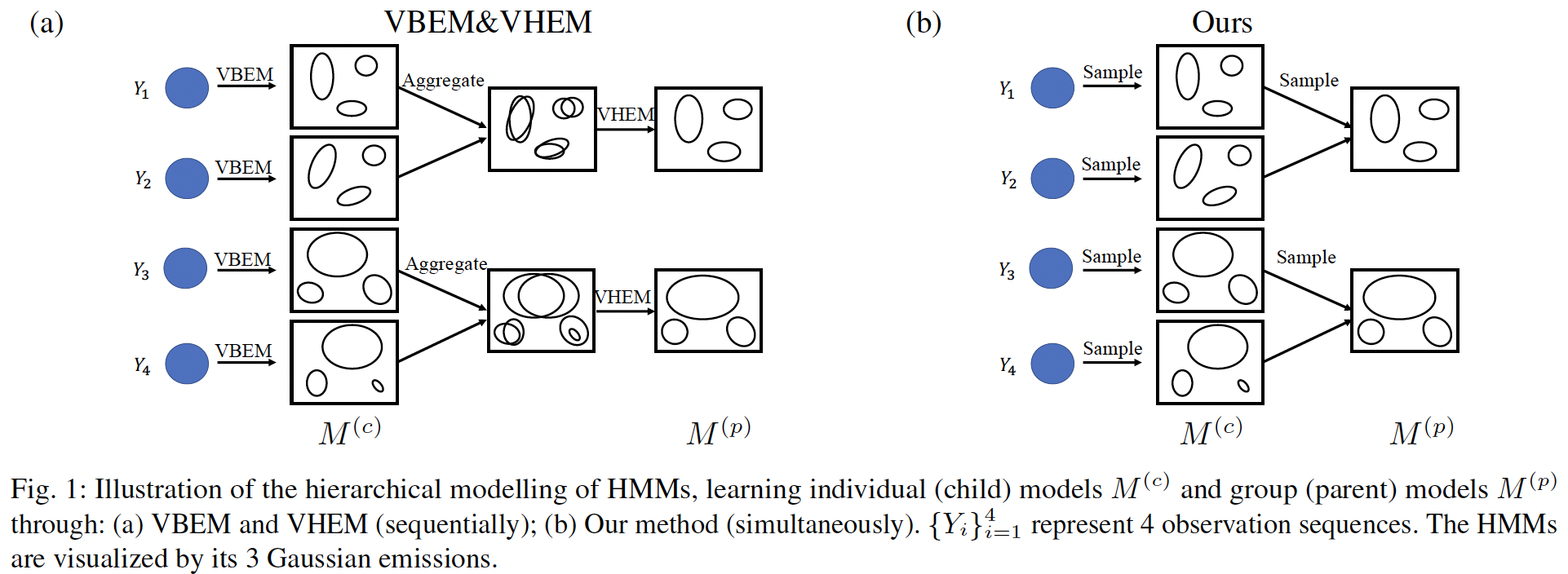
Hierarchical Learning of Hidden Markov Models with Clustering Regularization

The previous methods of hierarchical modelling of HMMs learn sequentially; first the individual models are learned from observations, then the group models are learned from the individual models, as shown in Fig. 1(a). Individual HMMs can be learned from observations using two typical methods: 1) the Baum-Welch (EM) algorithm, which computes the maximum likelihood parameter estimation of the HMM; 2) variational Bayesian EM (VBEM) algorithm, which computes the posterior distribution over each parameter of HMM through maximizing the evidence lower bound (ELBO). Learning the group models is equivalent to clustering individual HMMs, with each cluster center representing one group model. The variational hierarchical EM (VHEM) algorithm clusters HMMs directly using their probability densities of the observation sequence, and estimates HMM cluster centers.

In the above, the individual models and group models are learned as separate tasks. When the data is sufficient, separately learning individual and group models is fine. However, when the data is insufficient, the individual model may overfit, which affects the group model. For example, in face recognition or in scene perception, only one eye fixation sequence is tracked per stimulus. In this case, joint learning of individual and group models will help learning of individual models through pooling of common information in the group.

In this paper, we propose to estimate the individual and the group models simultaneously, as shown in Fig. 1(b), so that the group models can regularize the individual models. This is similar to the hierarchical generative process: 1) there are group models; 2) individual models are sampled from the group models; 3) observations are sampled from the individual models. This generative process is similar to topic model in document corpora, where documents are organized in a multi-level hierarchy. Although here we focus on HMMs, the framework could be applied to other probabilistic models.

Selected Publications