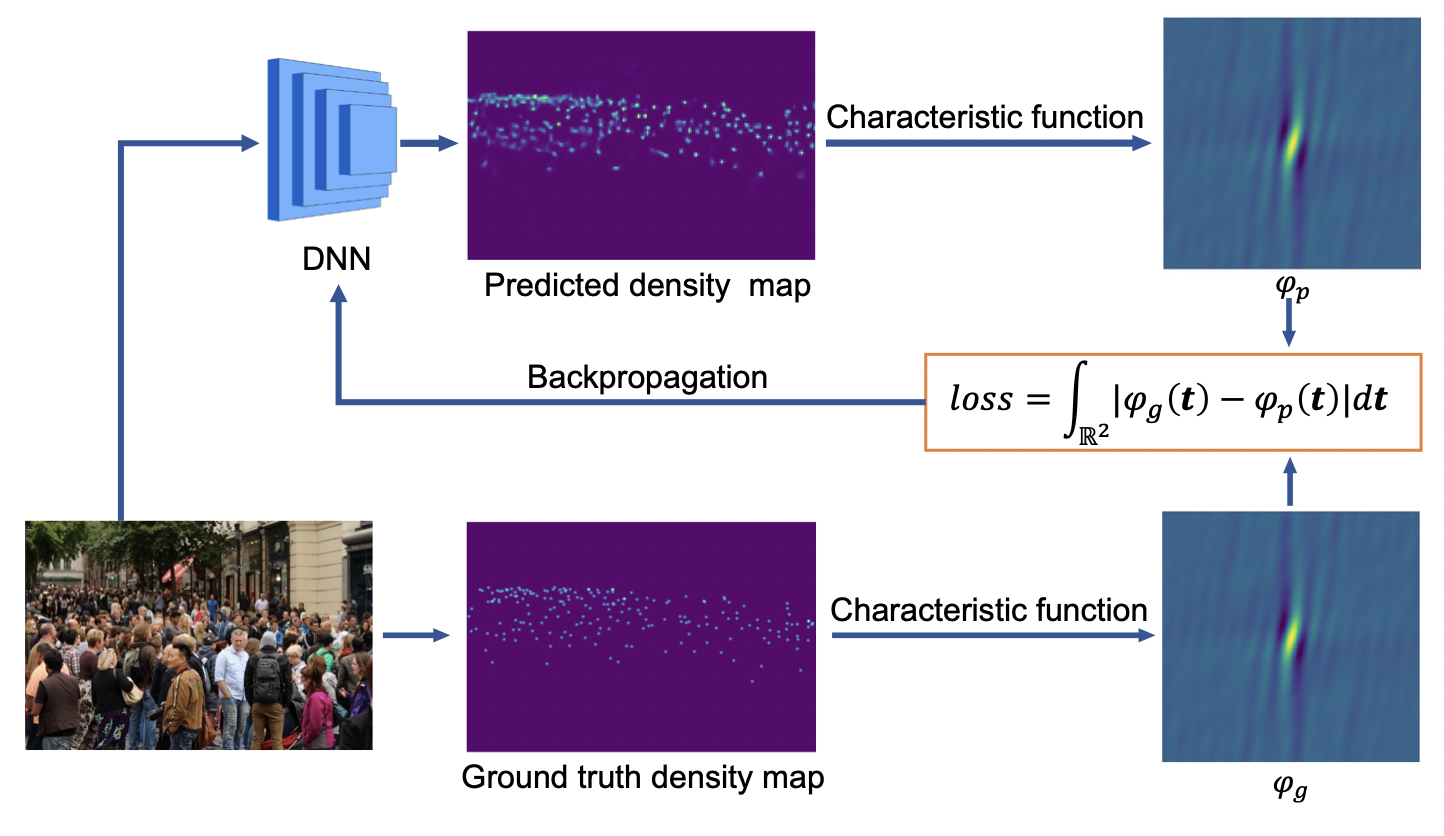
We investigate a new loss for crowd counting that fully harnesses both the position information and counting information of the ground truth. We hope the new method both provides the high-quality spatial supervisory information for training, and easily extracts it from the ground truth. Such properties may be hard to fulfill in the spatial domain, so instead we turn to an analysis in the frequency domain. Our solution is to use the characteristic functions of finite measures (i.e., unnormalized probability densities). It is intuitive that a density map is a finite measure on the 2D plane, and the position information and counting information are all in the finite measure. However, in the spatial domain, that information is spread out everywhere, and thus the global spatial information is hard to use without some external algorithms to extract it (e.g., the Sinkhorn algorithm for the optimal transport in DMcount and GeneralizedLoss, the Hungarian algorithm for the P2PNet). In contrast, if the finite measure is transformed into the frequency domain, then the spatial information is hierarchically organized in a compact range around the origin in the frequency domain. Values closer to the origin contain a larger proportion of global spatial information, while values further from the origin contain a larger proportion of local position information. Hence, a proper loss function on the frequency domain will adequately deliver all the information to the DNN for training. Our contributions are as follows:
- We extend the definition of the characteristic function from probability distributions to finite measures, as well as prove or intensify some of its vital properties. Thus, we transfer the learning problem from supervision with spatial density maps to supervision with frequency-domain characteristic functions, where the latter compactly summarizes the dispersed spatial information, which is more suitable for supervision.
- Using properties of the characteristic function, we propose a simple, effective, and efficient loss function that provides high-quality supervisory information for training, and, in contrast to previous works, does not require external algorithms for extracting spatial information.
- We prove that minimizing our loss function will decrease the upper bound of a pseudo sup norm metric between the predicted and the ground truth density map (over all sub-regions), which is effective for crowd counting.
- The experimental results on five benchmark datasets show our method’s competitiveness, and our loss function outperforms a large number of baseline and SOTA loss functions, while also being more efficient.
Selected Publications
- Crowd Counting in the Frequency Domain.
,
In: IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), June 2022.
Results
- Code is available here.
